HODMD(高阶动态模式分解)
标准动态模式分解的改进版本,主要利用高阶Koopman算子假设。
简介
示例
废话不多说,拿个toy来看看HODMD行不行。
这里我构建了一个多模态流体动力学仿真数据集,模拟了二维流场中多个物理模态的叠加演化过程,我将HODMD应用在此叠加的流场数据上,查看分解得到的模态与重构流场。
🦚 数据集基本信息
变量数量: 2个(U: 水平速度分量,V: 垂直速度分量)
空间网格: 60×60 均匀网格,范围 \([-1,1] \times [-1,1]\)
时间维度: 100个时间步,时间步长 \(\Delta t = 0.1\)
数据格式: 4维张量 $\text{Tensor}(2, 60, 60, 100)$
🌊 物理模态构成
数据集包含4个具有不同动力学特性的模态:
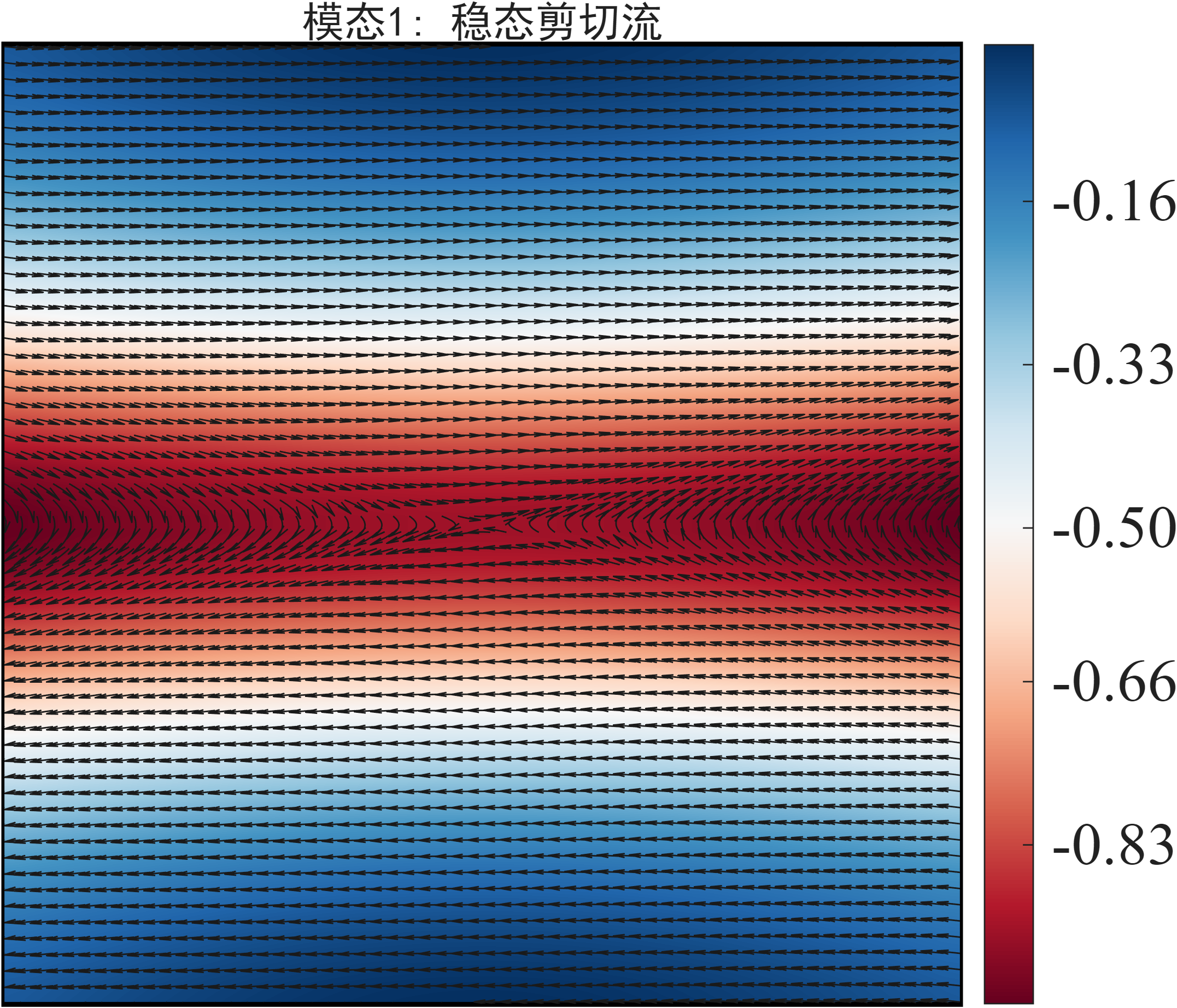
模态1: 稳态剪切流
频率: \(f_1 = 0 \text{ Hz}\)(稳态)
增长率: \(\sigma_1 = 0\)(中性稳定)
振幅: \(A_1 = 1.0\)
空间结构:
\(U_1(x,y) = \tanh\left(\frac{y}{0.5}\right)\)
\(V_1(x,y) = 0.1\sin\left(\frac{2\pi x}{4}\right)\)
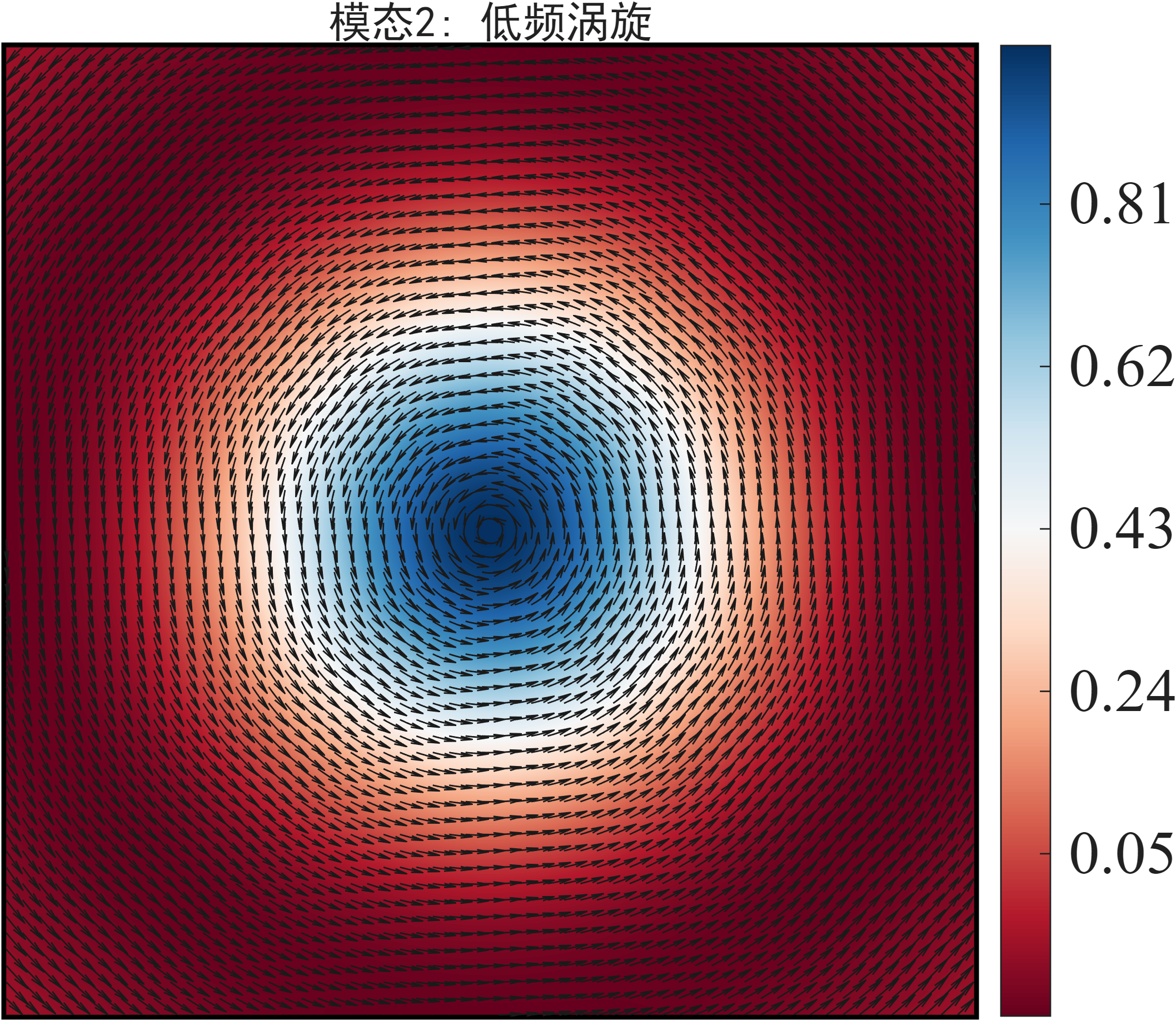
模态2: 低频涡旋
频率: \(f_2 = 0.2 \text{ Hz}\)
增长率: \(\sigma_2 = -0.02\)(轻微衰减)
振幅: \(A_2 = 0.3\)
空间结构:
\(U_2(x,y) = -y \cdot \exp\left(-\frac{x^2 + y^2}{0.5}\right)\)
\(V_2(x,y) = x \cdot \exp\left(-\frac{x^2 + y^2}{0.5}\right)\)
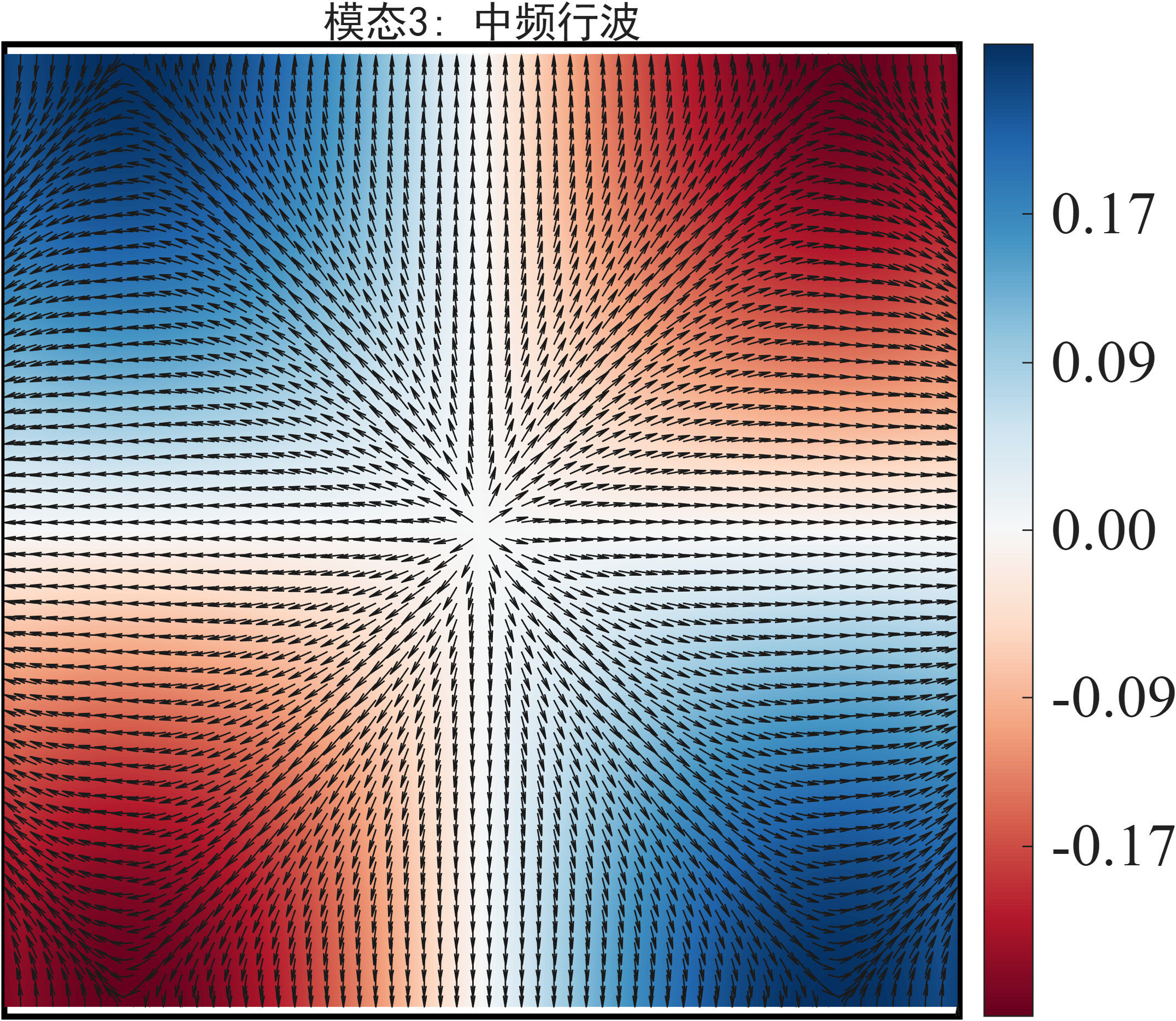
模态3: 中频行波
频率: \(f_3 = 0.5 \text{ Hz}\)
增长率: \(\sigma_3 = 0.01\)(轻微增长)
振幅: \(A_3 = 0.2\)
空间结构:
\(U_3(x,y) = \sin\left(\frac{2\pi x}{3}\right) \cdot \cos\left(\frac{\pi y}{2}\right)\)
\(V_3(x,y) = \cos\left(\frac{2\pi x}{3}\right) \cdot \sin\left(\frac{\pi y}{2}\right)\)
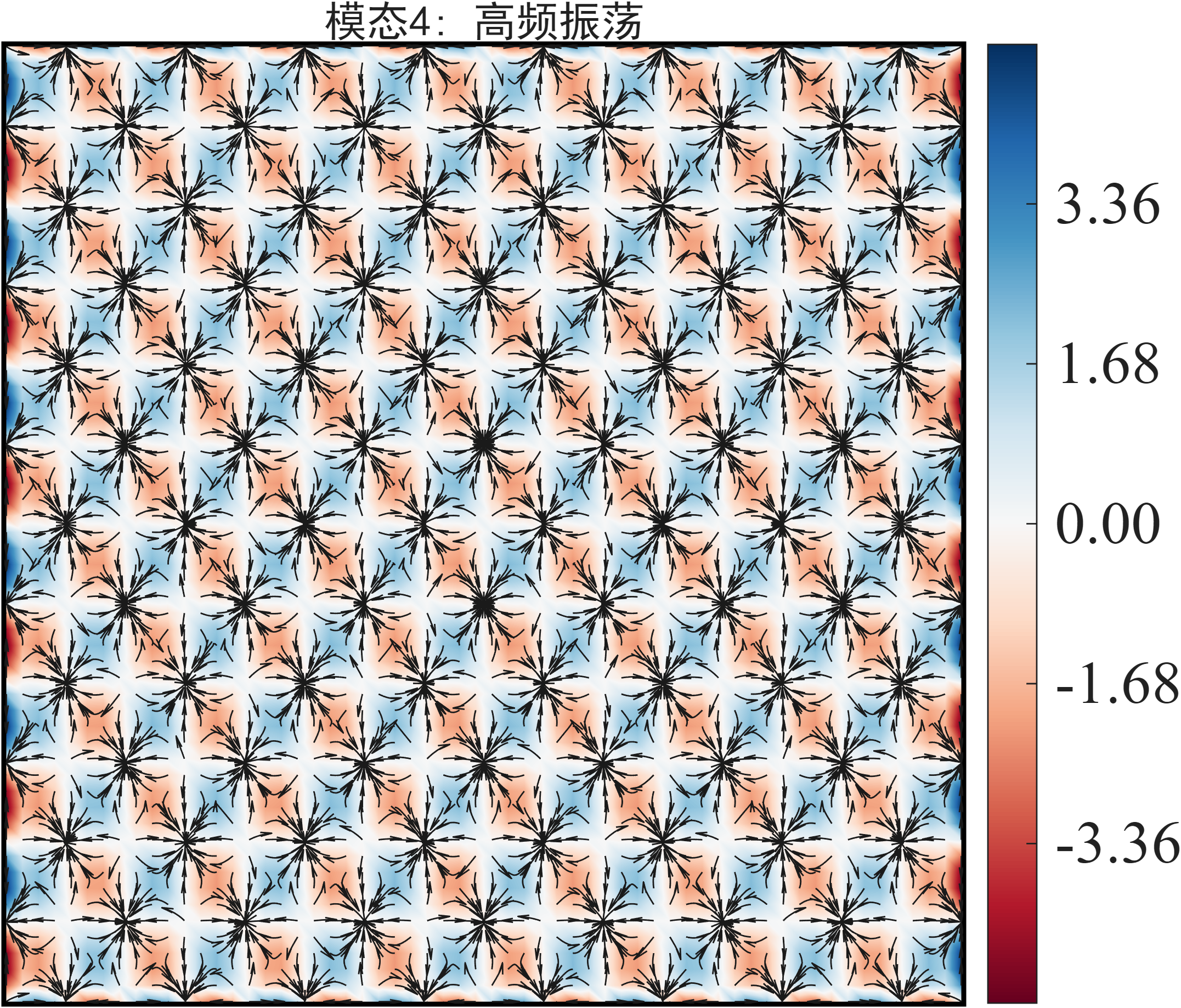
模态4: 高频振荡
频率: \(f_4 = 1.2 \text{ Hz}\)
增长率: \(\sigma_4 = -0.05\)(较强衰减)
振幅: \(A_4 = 0.15\)
空间结构:
\(U_4(x,y) = \sin(8\pi x) \cdot \cos(6\pi y)\)
\(V_4(x,y) = \cos(8\pi x) \cdot \sin(6\pi y)\)
⚙️ 数学表达
每个模态的时间演化遵循:
\(A_m(t) = a_m \cdot e^{(\sigma_m + i2\pi f_m)t}\)
总流场为各模态的线性叠加:
\(U(x,y,t) = \sum_{m=1}^{4} \text{Re}[A_m(t)] \cdot \Phi_m(x,y)\)
其中 \(\Phi_m(x,y) = [U_m(x,y), V_m(x,y)]^T\) 是第m个模态的空间结构。
👻实际模态离散特征值: \(\lambda=e^{(\sigma_m + i2\pi f_m)t}\)
| 模态 | 增长率 σ | 频率 |
|---|---|---|
| 模态1 | 1 | 0 |
| 模态2 | 0.990 | 0.125 |
| 模态3 | 0.952 | 0.309 |
| 模态4 | 0.725 | 0.681 |
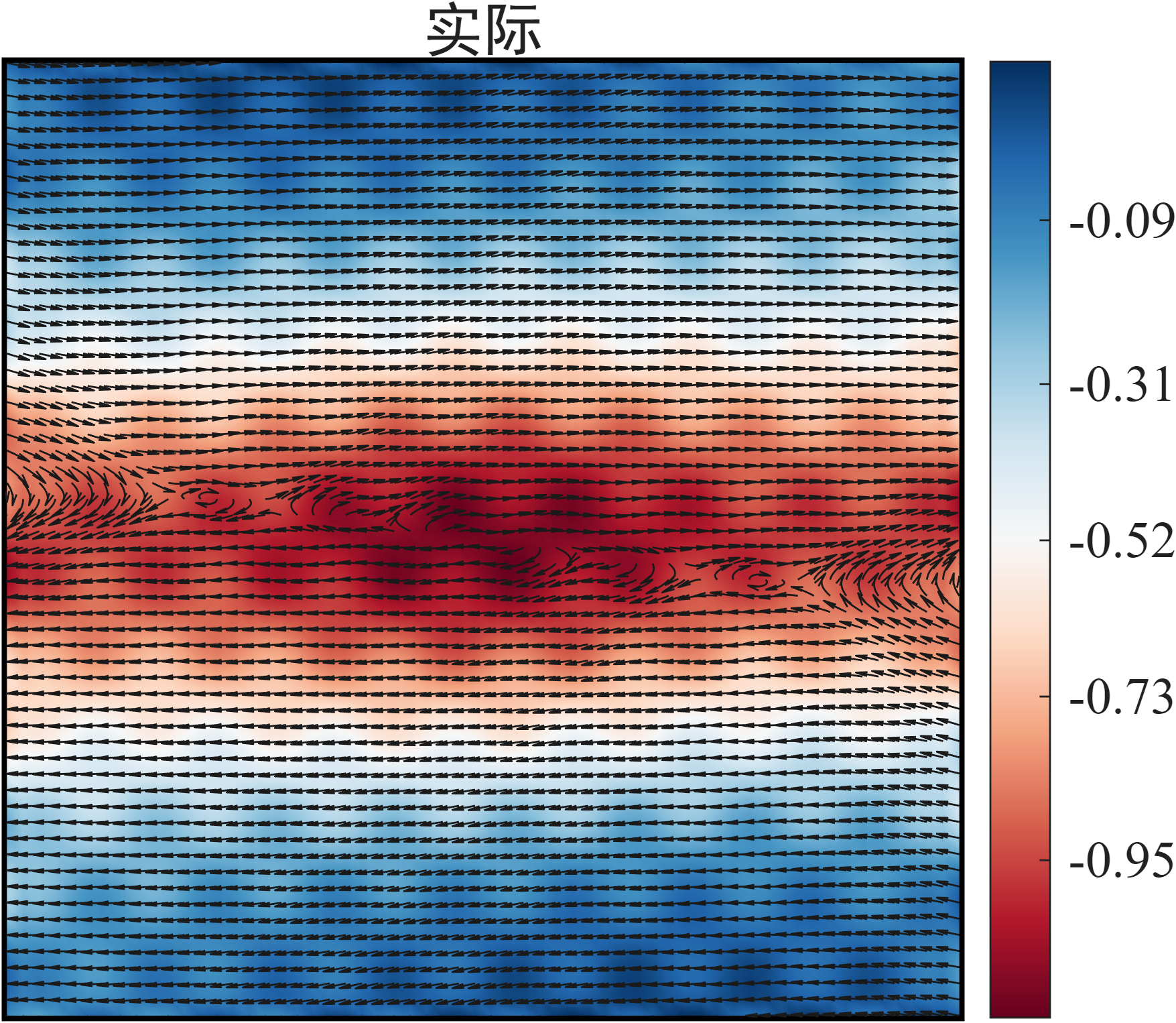
由于上面一个模态有两个空间结构,我这里把它们组成一个矢量,其中值表示模态涡量,并叠加流线矢量图。
下面是执行HODMD得到的模态结果:
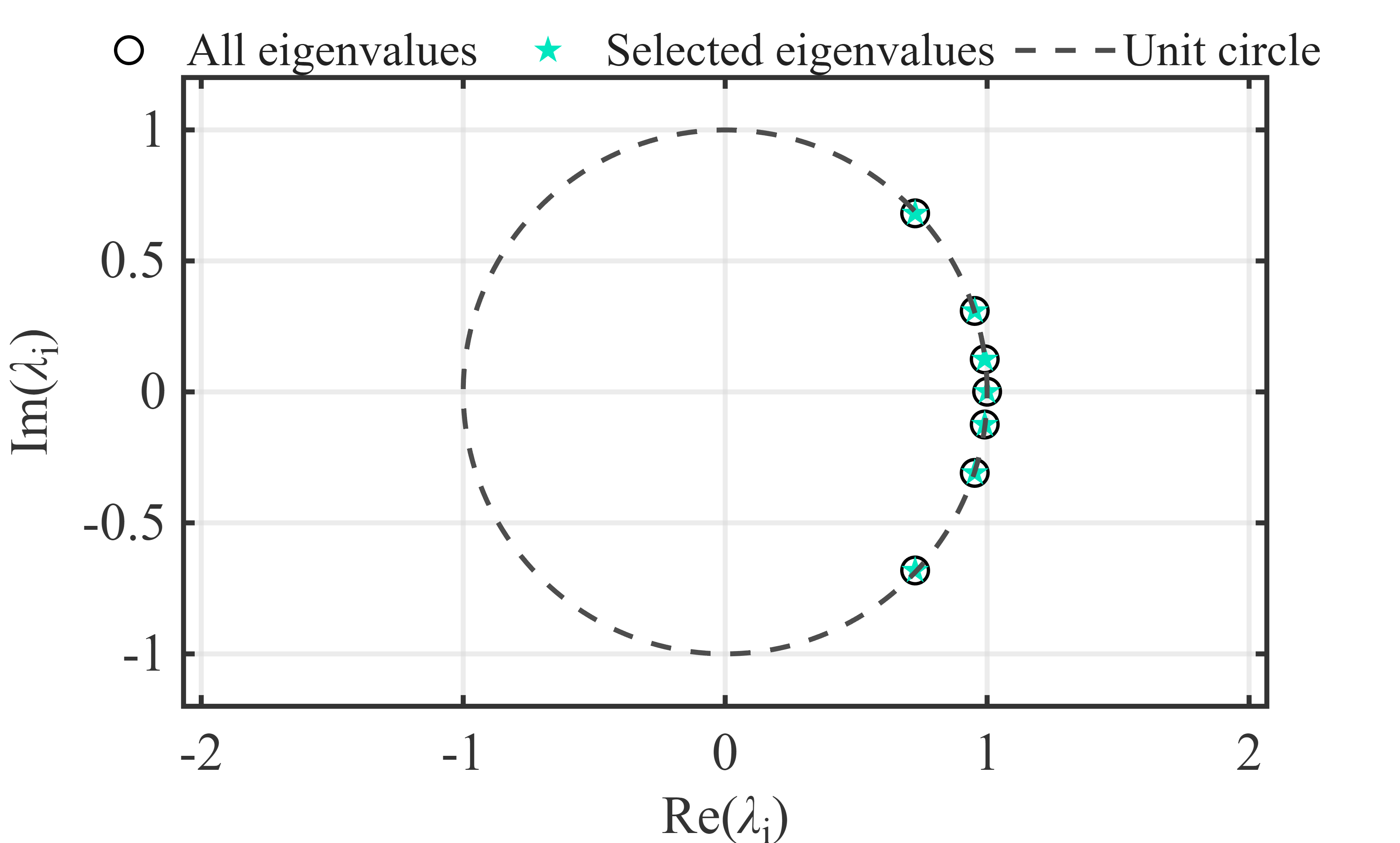
HODMD模态离散特征值: \(\lambda=e^{(\sigma_m + i2\pi f_m)t}\)
| 模态 | 增长率 σ | 频率 |
|---|---|---|
| 模态1 | 1 | 0 |
| 模态3 | 0.952 | 0.309 |
| 模态4 | 0.725 | 0.681 |
| 模态2 | 0.990 | 0.125 |
左图:离散特征值图;右图:连续特征值图。
可见提取出了与实际完全一样的增长率与频率的模态,只是模态不对应,当然这个不对应不是错误,而是实际模态的排序按照振幅进行,而这里HODMD模态的排序略有不同。 下面我们看看重构效果:
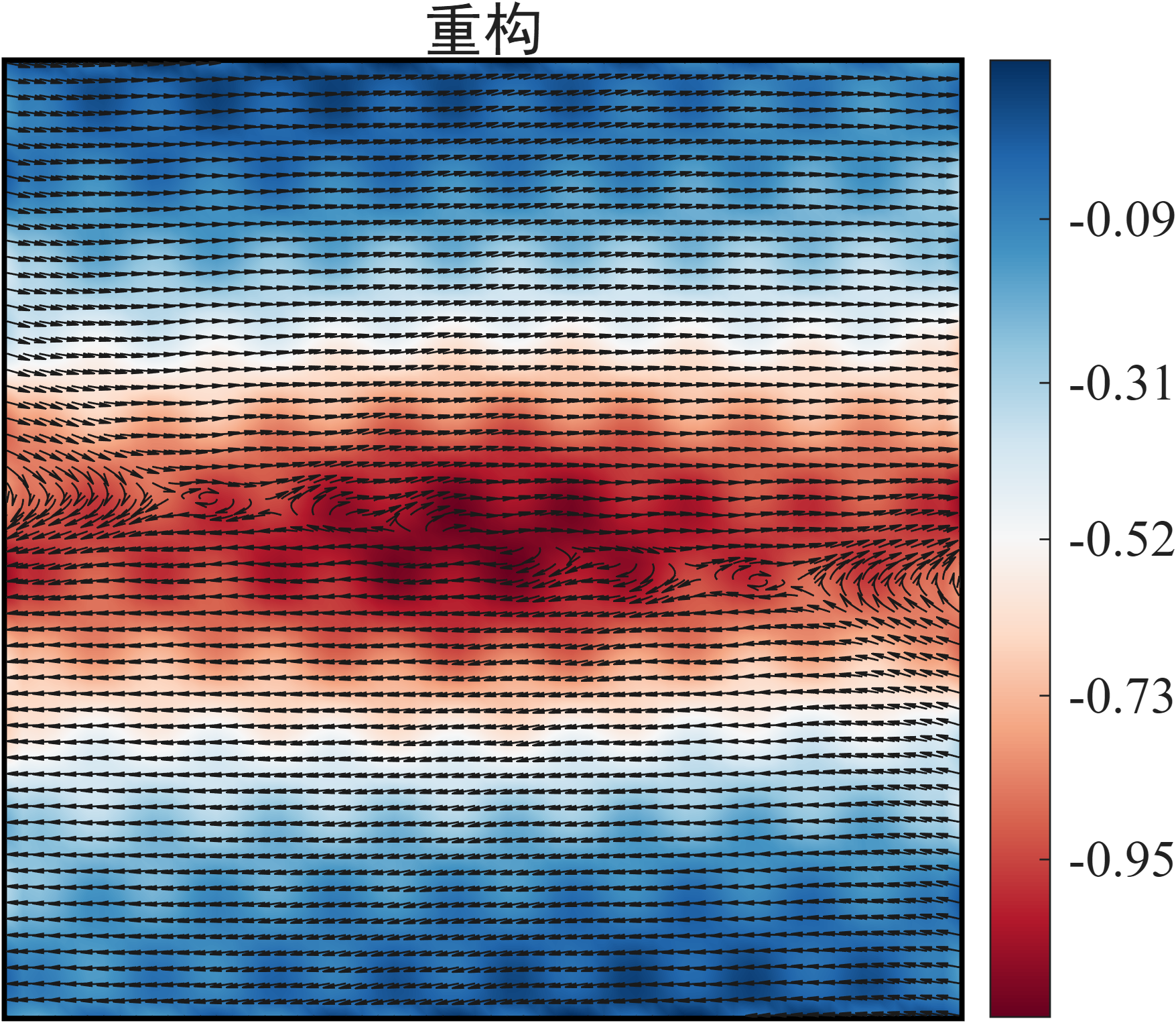
流场重构误差评估
变量定义
- 重构流场:\(\mathbf{U}_r = [u_r, v_r]^T\)
- 原始流场:\(\mathbf{U}_t = [u_t, v_t]^T\)
误差计算过程
1. 分量误差
\(e_u = u_r - u_t\) \(e_v = v_r - v_t\)
2. 误差模场
\(\varepsilon = \sqrt{e_u^2 + e_v^2}\)
3. 误差指标计算
均方根误差:
\(\varepsilon_{\text{rms}} = \sqrt{\text{mean}(\varepsilon^2)}\)
最大误差:
\(\varepsilon_{\text{max}} = \max(\varepsilon)\)
实际速度模场:
\(V_t = \sqrt{u_t^2 + v_t^2}\)
平均实际速度:
\(\bar{V}_t = \text{mean}(V_t)\)
相对误差:
\(\varepsilon_{\text{rel}} = \frac{\varepsilon_{\text{rms}}}{\bar{V}_t}\)
输出结果
均方根误差\(\varepsilon_{\text{rms}}\) = 2.8709e-14
最大误差\(\varepsilon_{\text{max}}\) = 4.4080e-14
相对误差\(\varepsilon_{\text{rel}}\) = 4.0633e-14
可见重构误差几乎很小,证明了HODMD的分解与重构的实力。